Pada pembahasan ini kita akan menemukan beberapa sifat khusus dari jajar genjang. Jajar genjang (parallelogram) adalah segi empat yang sisi-sisi yang saling berhadapannya sejajar.
Belah ketupat, persegi panjang, dan persegi memenuhi dari definisi jajar genjang di atas. Sehingga, semua sifat dari jajar genjang yang akan kita temukan nanti juga akan berlaku untuk bangun-bangun datar tersebut. Akan tetapi, untuk memastikan bahwa sifat-sifat yang kita temukan nanti berlaku untuk sembarang jajar genjang, kita sebaiknya menyelidiki jajar genjang yang tidak memiliki kekhususan, seperti sudutnya siku-siku, semua sudutnya sama besar, atau semua sisinya sama panjang.
Investigasi: Empat Sifat Jajar Genjang
Untuk melakukan investigasi ini, kamu memerlukan kertas berpetak, jangka, penggaris, dan busur derajat. Pertama-tama buatlah jajar genjang.
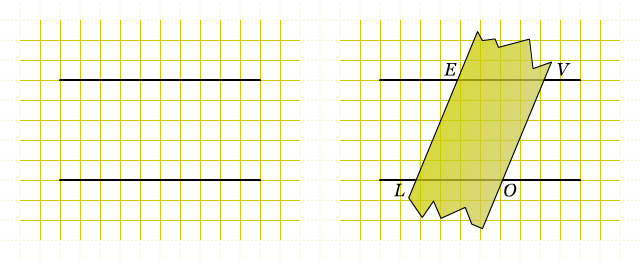
- Dengan menggunakan panduan garis pada kertas berpetak, buatlah sepasang garis sejajar yang jarakanya minimal 6 cm. Dengan menggunakan dua sisi sejajar pada penggaris, buatlah jajar genjang. Namai jajar genjang tersebut dengan LOVE.
- Mari kita perhatikan sudut-sudut yang berhadapan (opposite angles). Ukurlah sudut-sudut dalam jajar genjang LOVE. Bandingkan ukuran sudut-sudut yang berhadapan pada jajar genjang tersebut. Apa yang dapat kamu peroleh?
Kesimpulan: sudut-sudut yang berhadapan pada jajar genjang sama besar. - Dua sudut yang salah satu kakinya merupakan sisi yang sama pada poligon disebut sudut-sudut yang berdekatan (consecutive angles). Pada jajar genjang LOVE, sudutLOV dan sudut EVO merupakan pasangan sudut-sudut yang berdekatan. Hitunglah jumlah dari besar sudut dari setiap pasang sudut-sudut yang berdekatan pada jajar genjang LOVE. Apa yang dapat kamu simpulkan?
Kesimpulan: Besar sudut-sudut yang berdekatan pada jajar genjang adalah 180°. - Jelaskan bagaimana cara menentukan besar keempat sudut dalam jajar genjang apabila hanya diketahui besar salah satu sudutnya.
- Selanjutnya, perhatikan sisi-sisi yang berhadapan (opposite sides) pada jajar genjang. Dengan menggunakan jangka, bandingkan panjang dari sisi-sisi yang berhadapan pada jajar genjang yang telah kamu buat. Apa yang dapat kamu peroleh?
Kesimpulan: Sisi-sisi yang berhadapan pada jajar genjang adalah kongruen. - Dan akhirnya, perhatikan diagonal-diagonal dari jajar genjang. Lukislah diagonal-diagonal LV dan EO, seperti yang tampak pada gambar di bawah. Namai titik perpotongan kedua diagonal tersebut sebagai titik M.
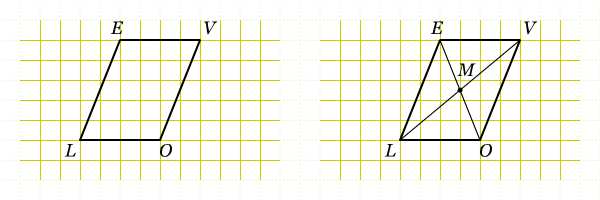
- Ukurlah LM dan VM. Apa yang dapat kamu simpulkan mengenai titik M? Apakah kesimpulan tersebut berlaku juga untuk diagonal EO? Apa hubungan dari kedua diagonal tersebut?
Kesimpulan: pada jajar genjang, kedua diagonalnya saling membagi dua sama panjang.
Jajar genjang digunakan dalam menggambar vektor, yang sering diterapkan pada sains.Vektor adalah besaran yang memiliki arah.
Pada bidang ilmu fisika, vektor mendeskripsikan kuantitas, seperti kecepatan, percepatan, dan gaya. Kamu dapat menggambarkan vektor sebagai garis panah. Panjang dan arah panah menunjukkan besar dan arah dari vektor tersebut. Misalnya, vektor kecepatan memberikan informasi mengenai kecepatan dan arah dari pesawat terbang. Panjang dari vektor pada gambar sebanding dengan kuantitas/nilai dari besaran yang digambarkan oleh vektor tersebut.
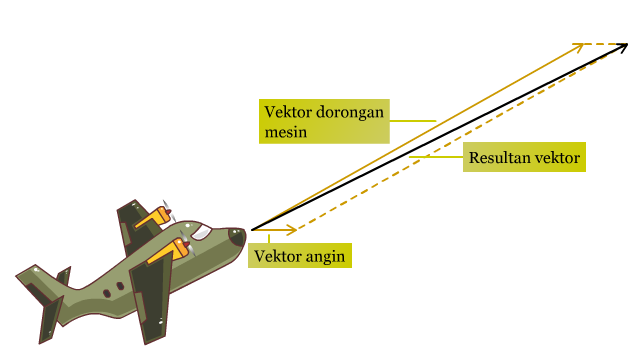
Pada beberapa permasalahan fisika, biasanya dikombinasikan beberapa besaran vektor untuk menunjukkan suatu kejadian. Misalkan, kondisi angin saat ini dan dorongan mesin yang digunakan untuk menentukan arah dan kecepatan terbang suatu pesawat. Vektor resultan dari vektor-vektor tersebut merupakan vektor tunggal yang memberikan efek yang sama terhadap suatu objek. Vektor resultan juga sering disebut jumlah vektor. Untuk menentukan vektor resultan, gambar suatu jajar genjang dengan vektor-vektor yang diberikan sebagai sisinya. Vektor resultan merupakan diagonal jajar genjang dari pangkal kedua vektor sampai ujung kedua vektor tersebut.
Tidak ada komentar:
Posting Komentar